Rapidly-Exploring Random Tree Star (RRT*)
RRT는 RRT의 최적화된 버전입니다. 노드의 수가 무한에 가까워질수록, RRT 알고리즘은 목표 지점까지의 최단 경로를 제공하게 됩니다. 현실적으로는 실현 불가능하더라도, 이 문장은 알고리즘이 최단 경로를 생성하는 방향으로 작동한다는 것을 의미합니다. RRT*의 기본 원리는 RRT와 동일하지만, 두 가지 기능이 추가되어 결과는 크게 발전합니다.
첫 번째, RRT*는 각 정점이 부모 정점으로부터 이동한 거리를 기록합니다. 이를 cost()라고 하며, 그래프에서 가장 가까운 노드가 찾아진 후, 새로운 노드로부터 일정 반경 내에 있는 이웃 노드들이 검사됩니다. 이 때, 근접 노드보다 더 적은 cost()를 지닌 노드가 발견되면, 그 근접 노드를 더 저렴한 새로운 노드로 대체하게 됩니다. 이 기능의 효과는 RRT의 정육면체 구조가 아닌 트리 구조의 부채꼴로 뻗어 나가는 가지들에서 확인할 수 있습니다.
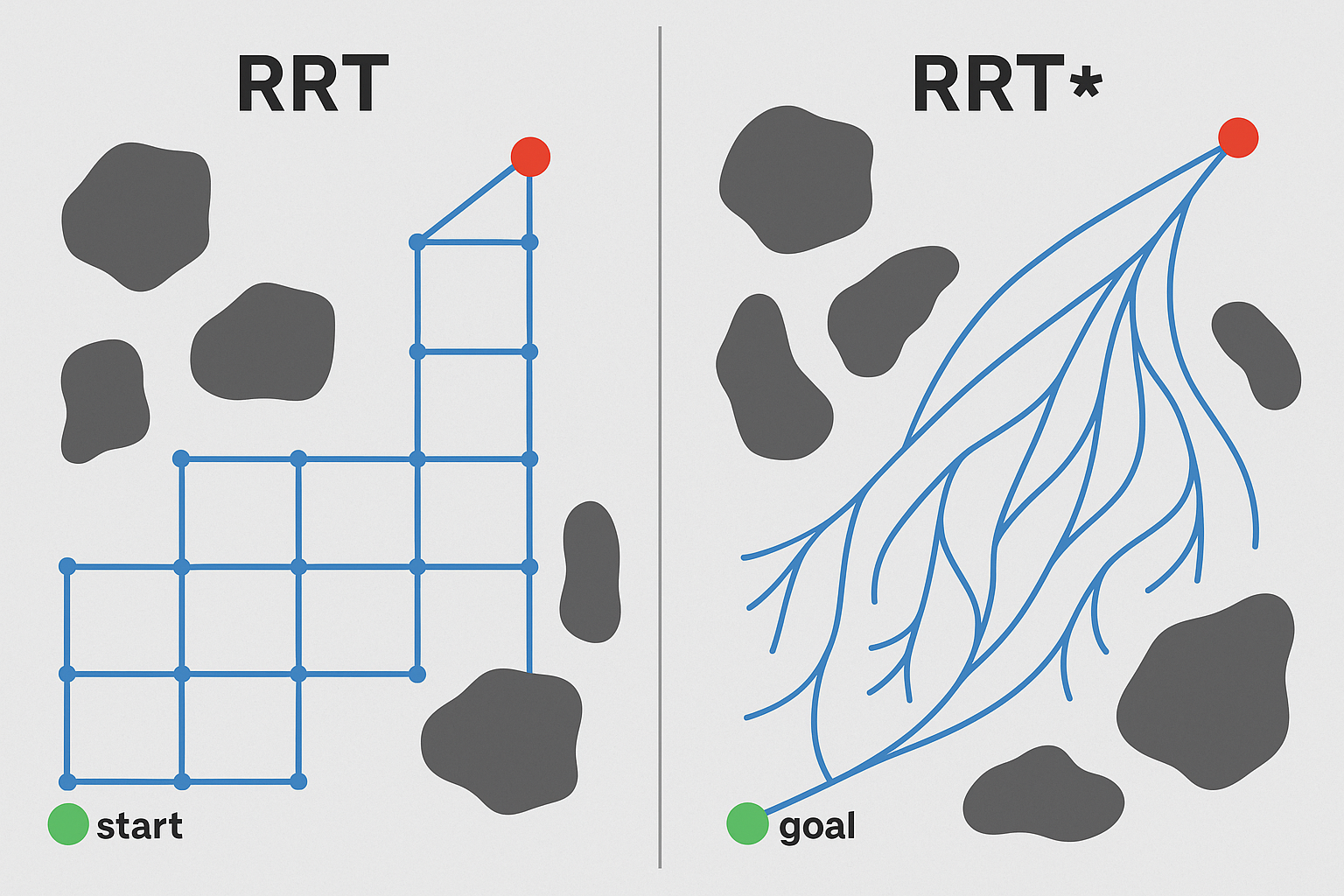
두 번째 차이점은 트리의 재배선(rewiring)입니다. 정점이 가장 저렴한 이웃 노드에 연결된 후, 이웃 노드들이 다시 한 번 검사됩니다. 이웃 노드가 새로 추가된 정점에 연결되었을 때, cost()가 줄어든다면, 해당 이웃 노드는 새 정점으로 다시 연결됩니다. 이 방법 덕분에 경로는 부드럽게 연결됩니다.
RRT는 매우 직선적인 경로를 만들언애며, 생성된 그래프는 RRT의 그래프와 다릅니다. 장애물이 많은 복잡한 환경에서 최적의 경로를 찾을 때, RRT의 구조는 매우 유용합니다. 목적지가 변경되더라도, 원래 생성된 그래프는 여전히 해당 영역 내 대부분의 위치에서 가장 빠른 경로를 나타내므로 활용이 가능합니다. 그럼에도 불구하고 RRT는 성능 저하라는 단점을 가지고 있습니다. 이웃 노드를 검사하고 그래프를 재배선해야 하기 때문입니다. 장애물 회피 여부를 확인하는 데에 드는 많은 소요 시간이 들지만, 생성된 경로의 우수성을 부정할 수 없습니다.
다음은 RRT*의 pseudo 코드입니다:
Rad = r
G(V,E)
For itr in range(0, n)
Xnew = RandomPosition()
If Obstacle(Xnew) == True, try again
Xnearest = Nearest(G(V,E), Xnew)
Cost(Xnew) = Distance(Xnew, Xnearest)
Xbest, Xneighbors = findNeighbors(G(V,E), Xnew, Rad)
Link = Chain(Xnew, Xbest)
For x` in Xneighbors
If Cost(Xnew) + Distance(Xnew,x`) < Cost(x`)
Cost(x`) = Cost(Xnew) + Distance(Xnew, x`)
Parent(x`) = Xnew
G += {Xnew, x`}
G += Link
return G
class Node:
def __init__(self, x, y):
self.x = x
self.y = y
self.parent = None
self.cost = 0.0
class RRTStar:
def __init__(self, start, goal, map_area, obstacle_lst, step_size=1.0, goal_sample_rate=0.1, max_iter=500):
self.start = Node(*start)
self.goal = Node(*goal)
self.map_area = map_area
self.obstacle_lst = obstacle_lst
self.step_size = step_size
self.goal_sample_rate = goal_sample_rate
slef.max_iter = max_iter
self.node_lst = [self.start]
self.search_radius = 5.0
def plan(self):
for i in range(self.max_iter):
rnd = self.sample()
nearest_node = self.get_nearest_node(rnd)
new_node = self.steer(nearest_node, rnd)
if not self.is_collision(new_node):
neighbors = self.find_neighbors(new_node)
min_cost_node = nearest_node
min_cost = nearest_node.cost + self.distance(nearest_node, new_node)
for neighbor in neighbors:
cost = neighbor.cost + self.distance(neighbor, new_node)
if not self.is_cllision_edge(neighbor, new_node) and cost < min_cost:
min_cost = cost
min_cost_node = neighbor
new_node.cost = min_cost
new_node.parent = min_cost_node
self.node_lst.append(new_node)
for neighbor in neighbors: #Rewire
cost_through_new = new_node.cost + self.distance(new_node, neighbor)
if cost_through_new < neighbor.cost and not self.is_collision_edge(new_node, neighbor):
neighbor.parent = new_node
neighbor.cost = cost_through_new
return self.extract_path()
def sample(self):
if random.random():
return self.goal
else:
x = random.uniform(self.map_area[0], self.map_area[1])
y = random.uniform(self.map_area[2], self.map_area[3])
return Node(x, y)
def get_nearest_node(self, node):
return min(self.node_list, key=lambda n: self.distance(n, node))
def steer(self, from_node, to_node):
dist = self.distance(from_node, to_node)
theta = math.atan2(to_node.y - from_node.y, to_node.x - from_node.x)
dist = min(self.step_size, dist)
new_node = Node(from_node.x + dist * math.cos(theta),
from_node.y + dist * math.sin(theta))
return new_node
def is_collision(self, node):
for (ox, oy, size) in self.obstacle_list:
dx = ox - node.x
dy = oy - node.y
if dx * dx + dy * dy <= size**2:
return True
return False
def is_collision_edge(self, n1, n2):
steps = int(self.distance(n1, n2) / 0.1)
for i in range(steps):
x = n1.x + i / steps * (n2.x - n1.x)
y = n1.y + i / steps * (n2.y - n1.y)
if self.is_collision(Node(x, y)):
return True
return False
def distance(self, n1, n2):
return math.hypot(n1.x - n2.x, n1.y - n2.y)
def find_neighbors(self, node):
radius = self.search_radius
return [n for n in self.node_list if self.distance(n, node) <= radius]
def extract_path(self):
last_node = min(self.node_list, key=lambda n: self.distance(n, self.goal))
path = [(last_node.x, last_node.y)]
while last_node.parent:
last_node = last_node.parent
path.append((last_node.x, last_node.y))
return path[::-1]
def draw(self, path=None):
fig, ax = plt.subplots()
for node in self.node_list:
if node.parent:
ax.plot([node.x, node.parent.x], [node.y, node.parent.y], "-g")
for (ox, oy, size) in self.obstacle_list:
circle = plt.Circle((ox, oy), size, color='k')
ax.add_patch(circle)
if path:
xs, ys = zip(*path)
ax.plot(xs, ys, '-r', linewidth=2)
ax.plot(self.start.x, self.start.y, "ro")
ax.plot(self.goal.x, self.goal.y, "bo")
ax.set_xlim(self.map_area[0], self.map_area[1])
ax.set_ylim(self.map_area[2], self.map_area[3])
ax.set_aspect('equal')
plt.title("RRT* Path Planning")
plt.grid(True)
plt.show()
if __name__ == "__main__":
start = (0,0)
goal = (20,20)
map_area(-5, 25, -5, 25)
obstacle = [] #predefined
rrt_star = RRTStar(start, goal, map_area, obstacles)
path = rrt_star.plan()
rrt_star.draw(path)
Reference: @misc{karaman2011samplingbasedalgorithmsoptimalmotion, title={Sampling-based Algorithms for Optimal Motion Planning}, author={Sertac Karaman and Emilio Frazzoli}, year={2011}, eprint={1105.1186}, archivePrefix={arXiv}, primaryClass={cs.RO}, url={https://arxiv.org/abs/1105.1186}, }
Enjoy Reading This Article?
Here are some more articles you might like to read next: