Rapidly-Exploring Random Trees

RRT, Rapidly-exploring Tree는 경로 계획 문제의 폭넓은 범주를 위해 설계된 랜덤화된 자료 구조입니다. RRT는 비홀로노믹 제약 조건과 높은 자유도를 처리할 수 있도록 설계되었으며, 무작위로 선택된 지점을 향해 시스템을 약간씩 이동시키는 제어 입력을 반복적으로 적용함으로써 확장됩니다. 이 글에서는 RRT의 기본 특성부터 구현까지 의논합니다.

RRT 이전, 여러 랜덤화 접근법들이 제안되었고, 그 중 랜덤화된 포텐셜 필드 알고리즘과 확률적 로드맵 알고리즘이 일반적인 경로 계획 문제에 성공적으로 적용되었습니다. 하지만 기존 기술들은 표준적인 경로 계획에는 강력하지만, 일반적으로 비홀로노믹 경로 계획 문제에는 자연스럽게 확장되지 않습니다. 상태 공간 표현을 사용하는 이 문제 범주는 운동역학적 경로 계획을 포함하며, 이는 로보틱스에서 일반적이고 중요한 영역입니다. 랜덤화 포텐셜 필드 방식은 좋은 휴리스틱 포텐셜 함수 선택에 크게 의존하는데, 이는 장애물, 운동학적 미분 제약, 동역학 제약이 있는 경우 상당히 어려운 작업이 됩니다. 확률적 로드맵 접근법에서는 구성 공간 내에서 무작위로 구성을 생성하고, 인접한 구성 쌍을 연결하기 위해 지역 계획자를 사용하여 그래프를 구축합니다. 하지만, 일반적으로 이 연결 문제는 비선형 제어기를 설계하는 것만큼이나 어렵습니다. RRT는 비홀로노믹 제약을 가진 문제를 위한 경로 계획에 적합한 랜덤화 자료구조입니다.

RRT는 점들을 무작위로 생성하고, 가장 가까운 노드에 연결합니다. 각 정점(vertex)가 생성될 때마다, 그 정점이 장애물 바깥에 위치하는지 확인해야 합니다. 또한, 해당 정점을 가장 가까운 이웃 노드에 연결할 때도 장애물을 피해야합니다. 알고리즘은 생성된 노드가 목표 영역 안에 도달하거나, 사전에 설정한 한계치에 도달하면 종료합니다. 무작위 위치와 이 때 생성된 정점을 연결하는 (chaining) 방식은 사용자의 선택에 달려있습니다. RRT는 구조적으로 정육면체 형태의 그래프를 만듭니다. 이는 각 노드가 가장 가까운 이웃에 연결되기 때문입니다. 이러한 구조는 최적 경로를 찾을 확률을 낮추는 원인이 됩니다. 예를 들자면, 두 점 사이의 대각선을 연결하는 대신, 삼각현의 직각변을 따라 이동하게 되어 경로가 더 길어집니다. 이를 해결하기 위한 알고리즘이 RRT*입니다. RRT의 장점은 빠른 속도와 간단한 구현입니다. 가장 많은 연산이 요구되는 부분은 가장 가까운 이웃 노드를 찾는 작업이며, 이 연산은 생성된 정점의 수에 따라 점점 더 부담이 커집니다.

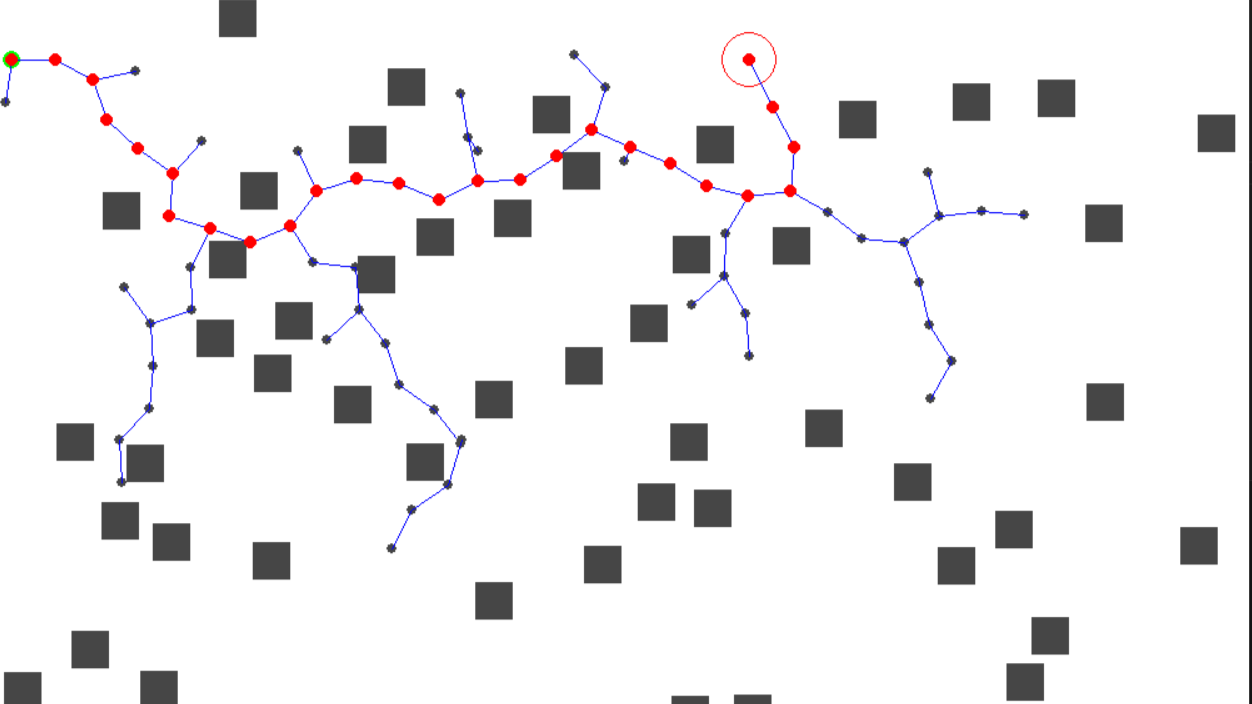
경로 계획은 일반적으로 메트릭 공간 $X$에서 초기 상태 $x_{init}$에서 목표 영역 $X_{goal} \subset X$ 또는 목표 상태 $x_{goal}$까지의 연속 경로를 탐색하는 것으로 간주됩니다. 여기서 상태 공간(state space)라는 용어는 경로 계획에서 보통 고려되는 것보다 더 일반적인 개념을 나타냅니다. 고정된 장애물 영역 $X_{obs} \subset X$이 존재한다고 가정하며, 이 영역은 피해야합니다. 하지만 $X_{obs}$의 명시적인 표현은 제공되지 않습니다. 주어진 상태가 이 영역에 포함되는지 여부만 확인할 수 있습니다. $X_{obs}$에 있는 상태는 속도 제한, 충돌 위치, 혹은 다양한 해석을 포함할 수 있으며 이는 응용에 따라 다르게 나타냅니다. RRT(Rapidly-exploring Random Tree)는 모든 꼭짓점이 자유 상태 공간 $X_{free} \subset X$ (즉, $X_{obs}$의 여집합)에 속하도록 구성된다. 또한 RRT의 각 간선은 전적으로 $X_{free}$ 내에 위치한 경로에 해당한다. 상태 전이 방정식은 비홀로노믹 제약을 나타내기 위해 $\dot{x} = f(x, u)$ 형태로 정의됩니다. 벡터 $u$는 입력의 집합 $U$에서 선택되며, $\dot{x}$는 시간에 따른 상태의 미분을 의미합니다. 고정된 시간 간격 $\Delta t$ 동안 함수 $f$를 적분함으로써, 초기 상태 $x$와 입력 $u$에 대해 다음 상태 $x_{new}$를 구할 수 있습니다. 홀로노믹의 경우, $f(x, u) = u$로 정의할 수 있으며, $|u| \leq 1$로 제한됩니다. 이는 모든 방향으로 시스템을 이동시킬 수 있음을 의미합니다. 반면, 비홀로노믹 문제에서는 선택된 $f$로 인해 다음 상태가 제약을 받습니다:

주어진 초기 상태 상태 $x_{init}$에 대해, 꼭짓점 수가 $K$인 RRT $\mathcal{T}$는 다음과 같은 알고리즘으로 생성됩니다:

    
GENERATE_RRT(x_init, K, dt)
    𝒯.init(x_init);
    for k = 1 to K do
        x_rand = RANDOM_STATE()
        x_near = NEAREST_NEIGHBOR(x_rand, 𝒯)
        u = SELECT_INPUT(x_rand, x_near)
        x_new = NEW_STATE(x_near, u, dt)
        𝒯.add_vertex(x_new)
        𝒯.add_edge(x_near, x_new, u)
    return 𝒯

ρ는 사태 공간 상의 거리 측정 기준을 나타내며, 트리 $\mathcal{T}$의 첫 번째 꼭짓점은 $x_{init} \in X_{free}$입니다. 각 반족에서 무작위 상태 $x_{rand}$는 유한한 공간이라 가정된 $X$에서 선택되며, ρ를 기준으로 $x_{rand}$에서 가장 가까운 꼭짓점 $x_{near}$를 찾습니다. 마지막으로, $x_{near}$에서 $x_{rand}$까지 거리를 최소화하는 입력 $u$를 선택하여 $x_{new}$가 $x_{free}$ 내에 있도록 합니다.

충돌 검출은 V-Clip같은 점진적 방법으로 수행될 수 있습니다. NEW STATE는 가능한 새 상태를 평가하기 위해 각 입력 $u$에 대해 호출되며 $U$가 유한하지 않은 경우 이산화하거나 최적화 기법을 사용할 수 있습니다. 입력 $u$를 적용하여 얻은 새 상태 $x_{new}$는 트리에 꼭짓점으로 추가되고 간선 $(x_{near}, x_{new})$는 $u$와 함께 기록됩니다.

import numpy as np
import matplotpib.pyplot as plt
import random

# initial setting
X_LIMITS = (0, 100)
Y_LIMITS = (0, 100)
STEP_SIZE = 1.0
NUM_VERTICES = 500
GOAL_RADIUS = 2.0

def distance(p1, p2):
    return np.linalg.norm(np.array(p1) - np.array(p2))

def random_state():
    return(
        random.uniform(*X_LIMITS),
        random.uniform(*Y_LIMITS)
        )

#find nearest node
def nearest_vertex(tree, x_rand):
    return min(tree, key=lambda v:distance(v, x_rand))

#calc new state (simple euler integration)
def new_state(x_near, x_rand, step_size=STEP_SIZE):
    direction = np.array(x_rand) - np.array(x_near)
    norm = np.linalg.norm(direction)
    if norm == 0:
        return x_near
    direction = direction / norm
    x_new = np.array(x_near) + direction * step_size
    return tuple(x_new)

#RRT
def generate_rrt(x_init, K=NUM_VERTICES):
    tree = [x_init]
    edges = []
    
    for _ in range (K):
        x_rand = random_state()
        x_near = nearest_vertex(tree,x_rand)
        x_new = new_state(x_near, x_rand)
        tree.append(x_new)
        edges.append((x_near, x_new))
        
    return tree, edges
    
def plot_rrt(tree, edges, x_init):
    plt.figure(figsize=(8,8))
    for (x1, x2) in edges:
        plt.plot([x1[0], x2[0]], [x1[1], x2[1]], 'b-', linewidth=0.5)
    plt.plot(x_init[0], x_init[1], 'ro', label='Start')
    plt.title("RRT in 2D Space")
    plt.xlim(X_LIMITS)
    plt.ylim(Y_LIMITS)
    plt.gca().set_aspect('equal')
    plt.grid(True)
    plt.legend()
    plt.show()
        
if __name__ = "__main__":
    x_init = (50,50)
    tree, edges = generate_rrt(x_init)
    plot_rrt(tree, edges, x_init)

쉽게 다시 한 번 정리하자면 RRT는 초기 위치를 안 상태에서, 무작위의 점들을 발생시키고 그 점들 중 하나로 이동합니다. 만약 장애물이 있다면 다시 한 번 무작위 점들 중 하나로 돌아오고, 이를 반복하여 목적 지점까지 도착하게하는 알고리즘입니다.

Reference: @article{LaValle1998RapidlyexploringRT, title={Rapidly-exploring random trees : a new tool for path planning}, author={Steven M. LaValle}, journal={The annual research report}, year={1998}, url={https://api.semanticscholar.org/CorpusID:14744621} }